Наибольший общий делитель двух натуральных чисел

Основы программирования
Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать. Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь. Подробнее...

Условие задачи 2.24

Задача 2.24
Даны два натуральных числа X и Y. Найдите наибольший общий делитель этих чисел и выведите на экран значение наибольшего общего делителя.

Эта простая задачка очень часто встречается в учебниках по программированию, поэтому я решил её рассмотреть. Если кто забыл, что такое натуральные числа, то см. здесь.

Также напомню, что такое наибольший общий делитель (сокращённо - НОД).

Наибольшим общим делителем двух чисел X и Y называется наибольшее число Z, на которое делятся без остатка оба числа X и Y.

Понятно, что для решения задачи нам нужен какой-то хитрый способ (алгоритм). Вот с него и начнём.

Алгоритм Евклида для нахождения НОД

Евклид (или Эвклид) - это древнегреческий математик, который жил примерно в 300 году до нашей эры. Сведений об Евклиде дошло до наших дней немного, но кое что всё-таки мы знаем.

Алгоритм Евклида - это один из самых древних и самых известных алгоритмов для вычисления наибольшего общего делителя двух целых чисел (или общей меры двух отрезков - вся математика зародилась из жизненной необходимости).

Этот алгоритм имеет множество практических и теоретических применений. Заключается он в следующем:

Есть пара чисел.
Отнимаем от большего числа меньшее, и получаем новую пару: меньшее число и разность между большим и меньшим.
Повторяем до тех пор, пока числа в паре не будут равны. Это и будет наибольший общий делитель.
Равенство рано или поздно будет в любом случае, так как любое натуральное число делится без остатка на 1.

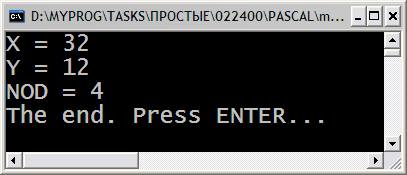
Теперь попробуем использовать алгоритм нахождения наибольшего общего делителя на каких-то определённых числах. Допустим, у нас есть числа 32 и 12. Тогда:

1) 32 - 12 = 20 (новая пара чисел 12 и 20) 2) 20 - 12 = 8 (новая пара чисел 12 и 8) 3) 12 - 8 = 4 (новая пара чисел 8 и 4) 4) 8 - 4 = 4 (новая пара чисел 4 и 4 - числа равны, следовательно, 4 - это НОД чисел 32 и 12)

Теперь осталось только составить программу нахождения наибольшего общего делителя. Сделаем это, как обычно, на Паскале и С++. Решим эту задачу с помощью цикла.

Решение задачи 2.24 на Паскале

 

program mytask;

//****************************************************************
// ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
//****************************************************************
var
  X   : Integer;
  Y   : Integer;

//****************************************************************
// ПОДПРОГРАММЫ
//****************************************************************
function Evklid(n1, n2 : Integer) : Integer;
begin
  while n1 <> n2 do
    begin
      if n1 > n2 then n1 := n1 - n2
      else n2 := n2 - n1;
    end;
  Result := n1;
end;

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
begin
  Write('X = '); ReadLn(X);
  Write('Y = '); ReadLn(Y);

  //На тот случай, если пользователь ввёл отрицательные числа
  X := Abs(X);
  Y := Abs(Y);

  WriteLn('NOD = ', Evklid(X, Y));

  WriteLn('The end. Press ENTER...');
  ReadLn;
end.

Решение задачи 2.24 на С++

#include <cstdlib>
#include <iostream>
#include <cmath>      //Для функции fabs

using namespace std;

//****************************************************************
// ГЛОБАЛЬНЫЕ ПЕРЕМЕННЫЕ
//****************************************************************
signed int X;
signed int Y;

//****************************************************************
// ПОДПРОГРАММЫ
//****************************************************************
signed int Evklid(signed int n1, signed int n2)
{
  while (n1 != n2)
    {
      if (n1 > n2) n1 = n1 - n2;
      else n2 = n2 - n1;
    }
  return(n1);
}  

//****************************************************************
// ОСНОВНАЯ ПРОГРАММА
//****************************************************************
int main(int argc, char *argv[])
{
  cout << "X = "; cin >> X; 
  cout << "Y = "; cin >> Y; 
  
  //На тот случай, если пользователь ввёл отрицательные числа
  X = abs(X);
  Y = abs(Y); 
  
  cout << "NOD = " << Evklid(X, Y) << endl;   
  
  system("PAUSE");
  return EXIT_SUCCESS;
}

Вступить в группу "Основы программирования"

Подписаться на канал в РУТУБ

Подписаться на Дзен-канал

Подписаться на рассылки по программированию

Как стать программистом 2.0

Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… Подробнее...

Помощь в технических вопросах

Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение - ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. Подробнее...

Главная
Контакты