Сложные математические формулы в программировании

Lazarus IDE: Основы программирования в Windows

Несмотря на то, что всё потихоньку уходит в сеть, программирование для настольных компьютеров остаётся востребованным. И будет таковым ещё долго. Ну а самая распространённая операционная система для настольных компьютеров – это по-прежнему Windows. Поэтому любой программист, даже если он собирается стать веб-разработчиком, должен знать хотя бы основы создания программ для Windows. Подробнее...

Недавно меня выгнали с работы, поэтому сейчас пытаюсь зарабатывать фрилансом. И вот подвернулась задачка - надо было перевести формулы с языка математики на язык программирования. В случае с простыми формулами это делается достаточно легко. Ведь операторы, такие как +, -, * и т.п. одинаково выглядят как в математике, так и в языках программирования.

Однако, если формулы достаточно сложные, то здесь уже становится не так весело. И времени на эту работу уходит достаточно много. И ошибок можно допустить немало, которые потом трудно выискивать.

Так что сегодня поделюсь своими хитростями работы с математическими формулами в программировании. Надеюсь, кому-нибудь окажется полезным.

Итак, вот пример такой формулы:

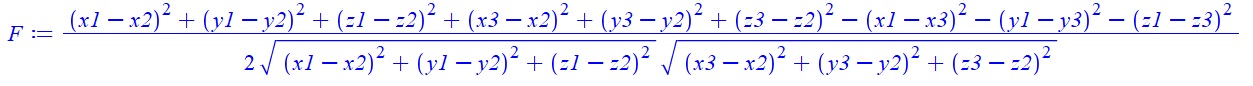
Выглядит довольно устрашающе. Но если взять себя в руки и отбросить панику, то можно её переписать на каком-нибудь языке программирования. Однако что делать, если таких формул у вас будет, например, 10. Похожих, но с небольшими отличиями. Неужели создавать 10 почти одинаковых функций?

Можно и так. Но лучше выделить в формулах повторяющиеся выражения и для каждого выражения создать отдельную функцию. А потом уже просто вызывать эти функции с необходимыми параметрами.

В итоге наша формула будет выглядеть примерно так:

Разбиение сложной формулы на отдельные выражения

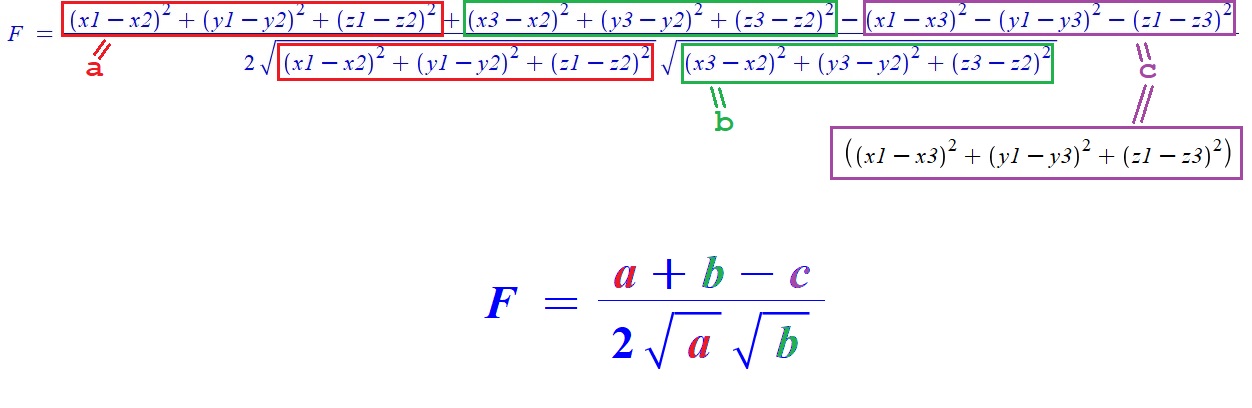
А вот так это может быть выполнено в исходном коде программы:

type Point3 = record
  x1, y1, z1 : Extended;
  x2, y2, z2 : Extended;
  x3, y3, z3 : Extended;
end;

// Вспомогательные функции
// (x1 - x2)^2 + (y1 - y2)^2 + (z1 - z2)^2
function a(p : Point3) : Extended;
begin
  Result := Sqr(p.x1 - p.x2) + Sqr(p.y1 - p.y2) + Sqr(p.z1 - p.z2);
end;

// (x3 - x2)^2 + (y3 - y2)^2 + (z3 - z2)^2
function b(p : Point3) : Extended;
begin
  Result := Sqr(p.x3 - p.x2) + Sqr(p.y3 - p.y2) + Sqr(p.z3 - p.z2);
end;
// (x1 - x3)^2 + (y1 - y3)^2 + (z1 - z3)^2
function c(p : Point3) : Extended;
begin
  Result := Sqr(p.x1 - p.x3) + Sqr(p.y1 - p.y3) + Sqr(p.z1 - p.z3);
end;

// F
function F(p : Point3) : Extended;
var chis, znam : Extended;
begin
  chis := (a(p) + b(p) - c(p));
  znam := 2 * Sqrt(a(p)) * Sqrt(b(p));
  Result := chis / znam;
end;

Ну и для закрепления рассмотрим ещё один пример, посложнее:

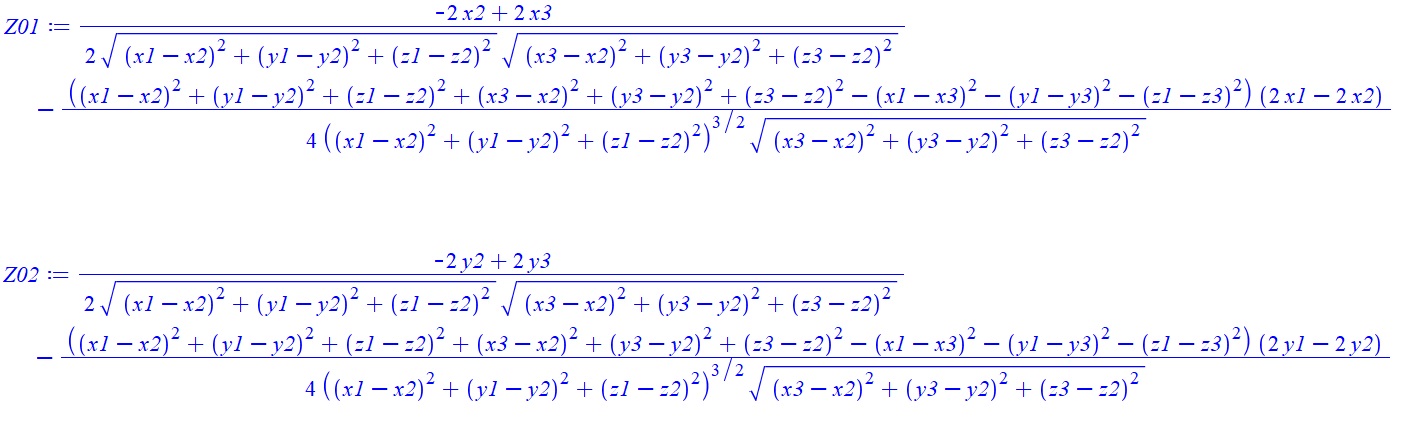
Здесь всё выглядит ещё страшнее. Но если присмотреться, то мы здесь увидим уже известные нам выражения, которые мы выделили в первом примере и назвали а, b и c. И эти выражения повторяются в функциях Z01 и Z02, Отличаются эти функции только двумя выражениями (на рисунке ниже я обозначил их как n1 и n2). Поэтому в нашей программе мы можем использовать уже готовые функции а, b и c в новых функциях Z01 и Z02, а упрощённая формула будет такой:

Тогда программный код может быть таким:

//Вспомогательная функция для вычисления Z01...Z2
function Za(p : Point3; n1, n2 : Extended) : Extended;
var r1, r2, r3 : Extended;
begin
	r1 := 2 * Sqrt(a(p)) * Sqrt(b(p));
	r2 := a(p) + b(p) - c(p);
	r3 := 4 * Exp(1.5 * Ln(a(p))) * sqrt(b(p));

  Result := (n1 / r1) - (r2 * n2 / r3);
end; 

// Z01
function Z01(p : Point3) : Extended;
var n1, n2 : Extended;
begin
  n1 := -2*p.x2 + 2*p.x3;
  n2 := 2*p.x1 - 2*p.x2;
  Result := Za(p, n1, n2);
end;

// Z02
function Z02(p : Point3) : Extended;
var n1, n2 : Extended;
begin
  n1 := -2*p.y2 + 2*p.y3;
	n2 := 2*p.y1 - 2*p.y2;
  Result := Za(p, n1, n2);
end;

Как видите, я добавил здесь вспомогательную функцию Za, чтобы уменьшить количество кода в функциях Z01 и Z02. Конечно, если у вас только две таких функции, то вспомогательные функции можно и не делать. Но если 10, 20 и больше, то такой подход существенно уменьшит количество исходного кода и размер исходного файла.

Ну и напоследок ещё один полезный совет - как не запутаться в скобках. В указанных выше примерах скобок не так много, поэтому запутаться сложно. Однако бывают и более навороченные формулы, где запутаться в скобках очень легко. Поэтому, если есть файл с формулами, то я преобразую его в формат рисунка (например, в JPG), открываю в графическом редакторе и там выделяю выражения и отмечаю скобки. Примерно так:

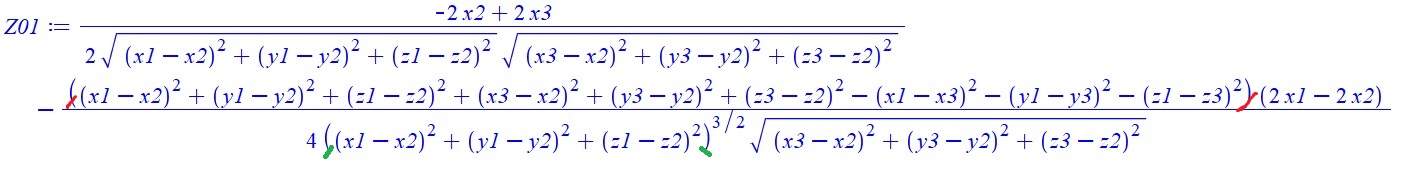
То есть открывающую и закрывающую скобку я выделяю одним цветом. Следующую пару скобок - другим цветом и так далее. И таким образом я выделяю в формуле выражения, которые потом можно перенести в исходный код программы.

Ну что же, на этом всё. Надеюсь, кому-нибудь это поможет сократить время на решение подобных задач. Математика в программировании - это не так уж скучно. Особенно если за это платят деньги )))

Вступить в группу "Основы программирования"

Подписаться на канал в РУТУБ

Подписаться на Дзен-канал

Подписаться на рассылки по программированию

Первые шаги в программирование

Очень небольшая книга, которую можно прочитать буквально за 15 минут. Но эти 15 минут дадут вам представление о том, что такое программирование. И вы даже напишите свою первую программу. Для тех, кто интересуется программированием, но ещё не знает, что это такое, и не пробовал создавать программы (или пробовал, но не получилось). Подробнее...

Помощь в технических вопросах

Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение - ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. Подробнее...

Главная
Контакты