Раздел: Курсы / Указатели /

Рекурсия

Куда указывают указатели Видеокурс для начинающих программистов. Вы узнаете, что такое динамические и статические структуры данных. Узнаете, что такое указатели и как с ними работать. Узнаете, как использовать память компьютера в своих программах, и как избежать ошибок, таких как утечки памяти. Кроме того, увидите реальные примеры, как и где применяются эти знания на практике. Подробнее...

В предыдущих своих книгах о программировании я старательно обходил тему рекурсии. Потому что, несмотря на то, что реализуется рекурсия довольно просто, сам принцип рекурсивного выполнения довольно сложен для понимания (я имею ввиду, конечно же, начинающих программистов).

Но время настало – дальнейшее изучение программирования без понимания рекурсии почти невозможно. Точнее, возможно, но теряет смысл. Сейчас именно тот момент, когда надо разобраться с рекурсивными методами обработки данных, так как без этих методов работа с бинарными деревьями почти невозможна.

Чтобы не отбить совсем у вас желание научиться программированию и не осложнить ещё более изучение темы рекурсии, я не буду углубляться в математику (хотя и надо бы). Если вам это интересно, то вспомните школьный курс математики и такое понятие как рекуррентная последовательность.

Примером рекуррентной последовательности являются, например, арифметическая прогрессия и геометрическая прогрессия.

То есть в рекуррентной последовательности содержится какое-то количество чисел (в общем случае – бесконечное). Каждое число в такой последовательности вычисляется через предыдущее число (или через ряд предыдущих чисел).

Например, есть такая арифметическая прогрессия:

1, 4, 7, 10, 13, 16, 19, …

Для вычисления всех чисел арифметической прогрессии нам надо знать только два параметра: первое число и число, которое прибавляется к первому числу для получения второго. То есть рекуррентная формула для нашей арифметической прогрессии:

a_i = a_i-1 + 3

Глубина рекурсии в таком случае равна 1, так как для получения следующего элемента в рекуррентной последовательности нам достаточно знать только значение одного предыдущего числа.

Для примера рассмотрим классический случай рекуррентной последовательности – числа Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

В этой последовательности каждое число, начиная с третьего элемента, равно сумме значений двух предыдущих. То есть глубина рекурсии здесь равна 2, так как для определения каждого элемента в последовательности необходимо знать значения двух предыдущих.

Формула для определения чисел Фибоначчи выглядит так:

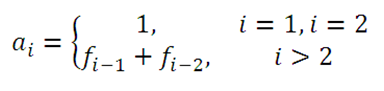
Надеюсь, вы знаете математику хотя бы на том уровне, чтобы понять эту формулу. Но на всякий случай поясню.

Каждое число в последовательности имеет порядковый номер (индекс) от 1 до бесконечности. Этот порядковый номер обозначается буквой i. Если i равно 1 или 2, то число в последовательности будет равно 1 (a₁ = 1, a₂ = 1). Если i > 2, то число вычисляется по формуле:

a_i = f_i-1 + f_i-2

Здесь буквой f обозначена функция, по которой выполняется вычисление. В нашем случае функция проста – она просто получает число с указанным индексом.

А теперь разберёмся с тем, как реализовать рекурсию в программировании, а конкретно на языке Паскаль.

Сделать это можно в цикле. Но практически во всех языках высокого уровня есть такая фишка, как рекурсивный вызов процедуры или функции. То есть такой вызов, при котором подпрограмма вызывает сама себя.

Пример использования рекурсивного вызова функции для вычисления чисел Фибоначчи приведён в листинге 3.3.

program ukaz;

{$mode objfpc}{$H+}

//**********************************************************************
// Вычисляет число Фибоначчи
//**********************************************************************
function Fibonachi(Num : integer) : integer;
begin
  if (Num = 1) or (Num = 2) then  //Если это 1-й или 2-й элемент
    Result := 1
  else                     //Иначе функция вызывает сама себя (рекурсия)
    Result := Fibonachi(Num-1) + Fibonachi(Num-2);
end;

var i : integer;

//**********************************************************************
// ОСНОВНАЯ ПРОГРАММА
//**********************************************************************
begin
  for i := 1 to 10 do
    Write(Fibonachi(i), ' ');
  ReadLn;
end.

Директивы компилятора Как это ни странно, но даже многие опытные программисты не используют директивы компилятора, считая их чем-то ненужным и бесполезным. А между тем, директивы компилятора - это очень классная штука. Если их умело применять в своих программах, то можно существенно сократить время на разработку и уменьшить количество рутинных операций. Подробнее...