Раздел: Стандартные функции Паскаля

Функция Power

Основы программирования Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать. Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь. Подробнее...

Функция Power в Паскале (и многих других языках программирования) выполняет возведение числа в степень.

Синтаксис для вещественных чисел:

function Power(Base: Double; Expon: Double) : Double;

Синтаксис для целых чисел:

function Power(Base: LongInt; Expon: LongInt) : LongInt;

Эта функция возводит число Base в степень Expon и возвращает результат. В реальности функция возвращает результат выражения:

Exp(Expon * Ln(Base))

Пример использования функции Power

Пример приведён ниже:

program funcpower;

uses Math;        

var x, y, z : single;

begin
  x := 2;
  y := 3;
  z := Power(x, y);   //Z = X в степени Y
  WriteLn(z:0:2);  

  ReadLn;
end.

Здесь мы число 2 (переменная Х) возводим в степень 3 (переменная Y), то есть вычисляем следующую формулу:

Z = XY

Обратите внимание на подключенный модуль MATH.

Эта статья входит в раздел о подпрограммах модуля SYSTEM. И по идее описания функции Power здесь не должно быть. Но, так как в документации сказано, что функция Power объявлена в модуле SYSTEM, я решил включить данную статью именно в этот раздел (я же не виноват, что в документации косяк))).

Возведение в степень в Паскале

Возведение в степень в Паскале можно выполнить и без какой-то специальной функции, используя функцию вычисления натурального логарифма и функцию вычисления экспоненты. О том, как это сделать, я рассказал здесь.

Однако, если есть специальная функция для возведения числа в степень, то почему бы ей и не воспользоваться? С одной стороны. С другой стороны - эта функция совершенно неожиданно требует подключения модуля MATH.

В документации сказано, что по сути функция Power работает по формуле возведения в степень в Паскале:

Exp(Expon * Ln(Base))

Однако, если мы будем делать именно так, эта формула будет неправильно работать с отрицательными числами, потому что в документации сказано, что функция Ln работает только с положительными числами.

Так что функция Power в реальности несколько сложнее, чем приведённая выше формула.

Поэтому для разминки мы напишем свой аналог функции Power, который будет работать правильно. Но для начала вспомним как вычисляется степень числа:

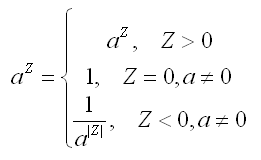
Также напомню, что любое число в нулевой степени равно 1, а ноль в любой степени равен 0 (кроме нуля в нулевой - ноль в нулевой степени не определён, но мы будем возвращать в таких случаях ноль, хотя функция Power возвращает 1).

А теперь наш аналог функции Power:

function AVPower(Base: Double; Expon: Double) : Double;
var m     : byte;
    i     : integer;
    Res   : Double;
begin
  m := 0;
  if Expon < 0 then m := 1              //Отрицательная степень
  else if Expon = 0 then m := 2         //Нулевая степень
       else m := 3;                     //Положительная степень
  if Base < 0 then m := 10 + m          //Отрицательное число
  else if Base = 0 then m := 20 + m     //Число равно 0
       else m := 30 + m;                //Положительное число
  case m of
  11  :   //Отрицательное число, отрицательная степень
    begin //Если Expon - не целое число, то получаются комплексные числа
      Res := 1 / Exp(Abs(Expon) * Ln(Abs(Base)));
      i := Round(Expon);
      if Odd(i) then Res := -1 * Res;
    end;
  12, 32  :   //Нулевая степень
    Res := 1;
  13  :   //Отрицательное число, положительная степень
    begin //Если Expon - не целое число, то получаются комплексные числа
      Res := Exp(Expon * Ln(Abs(Base)));
      i := Round(Expon);
      if Odd(i) then Res := -1 * Res;
    end;
  21..23  :   //Число равно нулю
    Res := 0;
  31  :       //Положительное число, отрицательная степень
    Res := 1 / Exp(Abs(Expon) * Ln(Base));
  33  :       //Положительное число, положительная степень
    Res := Exp(Expon * Ln(Base));
  end;     

  AVPower := Res;
end;

Я сознательно немного всё усложнил, чтобы вас запутать )))

Пример использования функций Power и её аналога в программе:

x := 2;
y := 3;
z := Power(x, y);     //Z = X в степени Y
WriteLn(z:0:2); 

z := AVPower(x, y);   //Z = X в степени Y
WriteLn(z:0:2);

Здесь есть один подвох - если вы попытаетесь возвести отрицательное число в не целую степень, например, так:

-2^3,5

то стандартная функция Power вызовет ошибку во время выполнения программы. В своём аналоге я этого избежал, но надо понимать, что результат в этом случае будет неправильным (хотя с моей точки зрения это всё-равно лучше, чем аварийное завершение программы).

Это происходит потому, что при таком раскладе результатом являются комплексные числа, а операции с комплексными числами выполняются по другим правилам.

В реальных программах подобные ситуации надо дополнительно обрабатывать (хотя бы предупреждать пользователя о том, что при отрицательном основании и не целой степени функция вернёт неправильный результат).

Ещё в моей функции используется функция Odd, о которой я ещё не рассказывал. Вкратце скажу, что она определяет, является ли число чётным. Более подробно о ней расскажу в отдельной статье.

Как стать программистом 2.0 Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… Подробнее...

Помощь в технических вопросах Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение - ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. Подробнее...